• Главная
• Новое
• Популярное
• Поиск
• Карта
• Связь

Таблицы выживания и таблицы размножения

Эволюционная экология / Принципы популяционной экологии / Таблицы выживания и таблицы размножения

Страница 2

В конечном счете нашу страховую компанию интересует оценка ожидаемой продолжительности жизни, или, другими словами, сколько еще в среднем проживет индивидуум, достигший возраста x. Для новорожденных особей (возраст 0) средняя ожидаемая продолжительность жизни равна средней продолжительности жизни когорты. Вообше ожидаемая продолжительность дальнейшей жизни в любом возрасте х — это просто средняя продолжительность оставшейся жизни индивидуумов, доживших до возраста х.

Английские термины «скорость рождаемости» (birth rate) и «скорость смертности» (death rate) в зависимости от контекста переводятся иногда как «рождаемость» и «смертность». — Прим. перев.

В формализованном виде данное положение может быть записано следующим образом: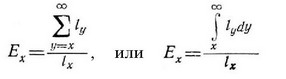

где Е — ожидаемая продолжительность жизни в возрасте х, а у — возраст. Первая приведенная форма уравнения дискретная, а вторая —непрерывная. Схема расчета Е приведена в табл. 5.1. .Мужчинам выплачивается более высокая страховая премия.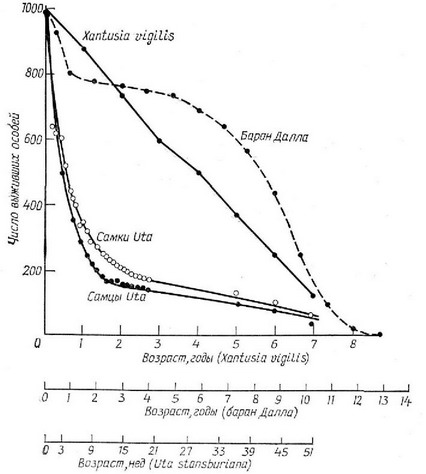

Рис. 5.2. Несколько кривых выживания в арифметическом масштабе (сравните их с сильно выпуклыми кривыми при представлении данных в полулогарифмическом масштабе, как это показано на рис. 5.3). Хотя обычно пользуются и теми и другими графиками, предпочтение все же следует отдать полулогарифмическим. График, характеризующий выживаемость ящерицы Xantusia, в арифметическом масштабе имеет вид диагональной прямой, а в полулогарифмическом — сильно выпуклой кривой, тогда как для другого вида ящериц (Uta) кривая выживаемости в арифметическом масштабе имеет вид гиперболы, а в полулогарифмическом масштабе — вид диагональной прямой. (По Deevey, 1947; Tinkle, 1967; Zweifel, Lowe, 1966.)

Таблица 5.1. Пример подсчета Е, Т, и в гипотетической стабильной популяции с дискретными возрастными классами по уравнениям (1) — (4)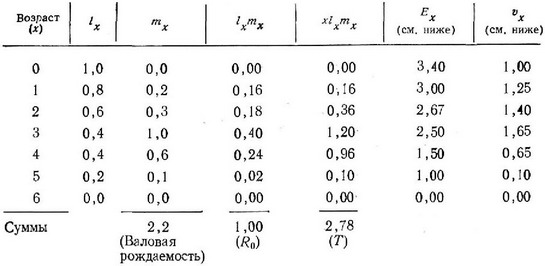

чем женщинам, так как кривая выживания первых падает более резко и, следовательно, для любого заданного возраста ожидаемая продолжительность жизни мужчин меньше, чем женщин. На рисунках 5.2 и 5.3 показаны некоторые кривые выживания,

Ожидаемая продолжительность жизни:

Репродуктивная ценность:

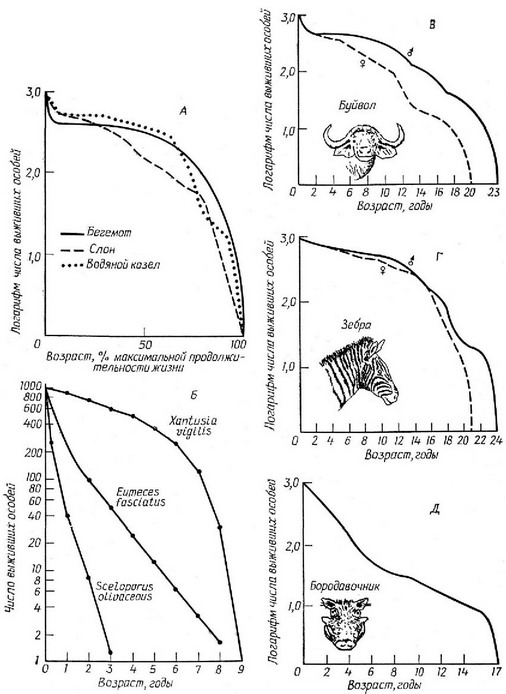
Рис. 5.3. Кривые выживания для некоторых видов животных, представленные в полулогарифмическом масштабе. Сравните кривую для Xantusia (Б) с кривой для этого вида на рис. 5.2, построенной но тем же самым данным. Преимущество полулогарифмической шкалы в том, что прямая на таком графике соответствует одинаковой смертности в любом возрасте. (По Zweifel, Lowe, 1966; Spinage, 1972; последняя ссылка с разрешения Duke University Press.)

иллюстрирующие большое их разнообразие, наблюдаемое в природных популяциях. Сильно выпуклая кривая выживания (образующая в полулогарифмическом масштабе почти прямой угол) отражает ситуацию, при которой смертность до определенного возраста очень низкая, а затем чрезвычайно быстро возрастает. Такая кривая, называемая кривой выживания типа I (Pearl, 1928), характерна для ящериц Xantusia vigilis и Scincella laterale, барана Дал-ла, большинства африканских копытных, человека и, по-видимому, вообще для большинства млекопитающих (Caughley, 1966). При относительно постоянной для разных возрастов смертности полулогарифмические кривые имеют вид диагонали (кривые типа П); такие кривые характерны для некоторых ящериц (Uta stansburia-па и Eumeces fasciatus), бородавочника и большинства птиц. На самом деле существуют два вида кривых типа П, соответствующие постоянной вероятности умереть в единицу времени и постоянному числу смертей в единицу времени (Slobodkin, 1962). У многих рыб, морских беспозвоночных, большинства насекомых, а также у многих растений смертность на ранних стадиях развития очень высокая, а в более поздний период — низкая, что отражается кривой выживания типа П1, напоминающей вогнутую гиперболу. Конечно, все встречающиеся в природе случаи нельзя втиснуть в узкие рамки трех или четырех удобных категорий, и между выделенными «типичными кривыми» существует целый ряд промежуточных. Кроме того, таблицы выживания не постоянны, а изменяются в зависимости от конкретных условий существования. Позднее мы рассмотрим эволюцию смертности и старения, но сначала необходимо обратиться к другому важному для популяции процессу — размножению.