Специфическая скорость естественного увеличения популяцииЭволюционная экология / Принципы популяционной экологии / Специфическая скорость естественного увеличения популяцииСтраница 1
Другой полезный показатель, скрытый в каждой паре таблиц рождений и смертей, — врожденная (специфическая) скорость естественного увеличения популяции, называемая иногда мальтузианским параметром. Эта величина, обозначаемая обычно буквой г, является мерой мгновенной удельной (в расчете на одну особь) скорости изменения размера популяции и выражается как число особей па единицу времени и па одну особь, т. е. имеет размерность 1/время. В замкнутой популяции специфическая скорость увеличения определяется как мгновенная удельная рождаемость Ь минус мгновенная удельная смертность й. В незамкнутой популяции г = (рождаемость + иммиграция) — (смертпость+эмиграция). Когда удельная рождаемость превышает удельную смертность, популяция растет и г положительпо, когда смертность превышает рождаемость (Ь<с1), г отрицательно и популяция сокращается.
На практике г довольно трудно вычислить и можно получить лишь ее оценку итерационным методом, используя способ Эйлера: 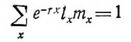
где е — основание натурального логарифма, ах— возраст. Вывод этого уравнения можно найти в других работах. При условии, что чистая скорость размножения примерно равна единице, значение г можно приблизительно рассчитать по формуле 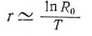
где Г— время генерации, определенное по уравнению (2) (см. также May, 1976). Из уравнения (9) следует, что г имеет положительное значение, если и отрицательное, если Д<1. Поскольку 1п1 = 0, равенство соответствует равенству г = 0. При оптимальных условиях, когда значение Rg максимально высоко, популяция характеризуется максимальной скоростью естественного увеличения, обозначаемой через г. Заметьте, что специфическая скорость увеличения обратно пропорциопальпа времени геперации Т (см. также рис. 5.27, с. 159).
Максимальная мгновенная удельная скорость увеличения популяции г варьирует у различных животных в пределах нескольких порядков (табл. 5.2). Мелкие, недолго живущие организмы, например такие, как обычная кищечпая палочка Escherichia coli, характеризуются довольно высокими значениями тогда как крупные организмы с большой продолжительностью жизпи, например человек, имеют сравнительно низкие значения г. Компоненты г — это мгновенная удельная рождаемость b и мгповеппая удельная смертность d, наблюдаемые в наиболее оптимальных условиях среды. Эволюция скорости размножения и смертности будет рассмотрена в этой главе ниже.
Любая популяция, числеппость которой линейно увеличивается со временем, имеет постоянную скорость увеличения: 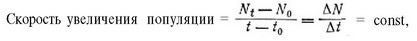
где ж, — число особей в момент времени 1, — начальное число особей, — начальный момент времени.
Однако если г — любая постоянная положительная величина (т. е. удельная скорость увеличения популяции постоянна), то популяция растет по экспопепциальпому закону (рис. 5.7). Скорость увеличения такой популяции зависит от ее численности, и чем больше М, тем быстрее она увеличивается. Предположим, что вы хотите определить скорость изменения численности популяции, показанной па рис. 5.7, в какой-то момент времени 1. При первом приближении можно оценить величину N пепосредствеппо перед моментом г и после пего, например за час до г и па час позже применив приведеппое выше уравнение ЛМ/Л. Однако, обратившись к рис. 5.7, мы видим, что в момент (например, 1ч) истиппая скорость на самом деле меньше, а в момент
Таблица 5.2. Оценки максимальной мгновенной скорости естественного увеличения популяции на особь за сутки) и среднее время генерации для различных организмов 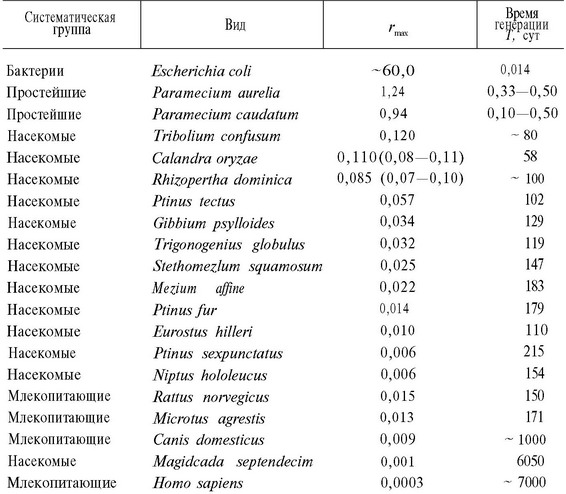
больше, чем при использованной памп линейной экстраполяции. При анализе подобных случаев применяется дифференциальное исчисление, позволяющее вычислить мгновенную скорость изменения в любой момент времени. По мере того как ЛЫ и Л становятся все меньше и меньше, отношение AN/At все больше приближается к истинной оценке скорости в момент времени 1 (рис. 5.7). В пределе, когда интервал Л приближается к нулю, АМ/А записывается как йЫ/сИ, что означает мгновенную скорость изменения N в момент Экспоненциальный рост популяции записывается простым дифференциальным уравнением: 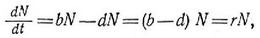
Смотрите также
Взаимодействие климата и растительности
Климат — главный фактор, определяющий характер растительности. Растения в свою
очередь также в некоторой степени воздействуют на климат. Как климат, так и растительность
оказывают решающее влияние ...
Особенности природоохранной деятельности в России.
В нашей стране на первом этапе становления хозяйственного
механизма природопользования недостатки административной системы руководства
проявлялись более явно и отчетливо, чем в других странах. ...
Экологическая ниша
Понятие ниши пронизывает все сферы экологии. Если бы термину «экологическая ниша»
не придавали так много самых разных значений, то экологию можно было бы определить
как науку о нишах. Многие аспек ...